Математические софизмы

Автор: Овчинникова Лариса Юрьевна

Организация: МКОУ Тогучинского района «Дергоусовская основная школа»

Населенный пункт: Новосибирская область, с. Дергоусово

Автор: Гейн Эльвира Геннадьевна

Организация: МКОУ Тогучинского района «Дергоусовская основная школа»

Населенный пункт: Новосибирская область, с. Дергоусово

«Дважды два равно пяти» - каждый из нас слышал такие фразы хоть раз в жизни. Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение? Именно эти вопросы я хочу рассмотреть в своей работе.

Я полагаю, что применение софизмов на уроках математики могли бы помочь вызвать интерес учащихся к предмету и разнообразить уроки.

Цель: Узнать, что такое математические софизмы.

Задачи проекта:                                             

1. Познакомиться с понятием – софизм.
2. Узнать виды математических софизмов.
3. Рассмотреть примеры математических софизмов.
4. Составить свой математический софизм.
5. Понять где используются математические софизмы.
6. Создать сборник задач «Математические софизмы».

Гипотеза: софизм – это искусно замаскированные  ошибки

Объёкт исследования: софизмы, их виды.

Предмет исследования: математические софизмы.

Софизм - это утверждение (умозаключение), выдаваемое за правильное, в котором допущена, умело замаскированная ошибка.

В математике очень много неожиданных и интересных софизмов, некоторые из них послужили толчком к новым открытиям

Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и алгебраических выражениях.

Пример:«Любое число а равно меньшему числу b».

  Арифметические софизмы- это числовые выражения имеющие неточность или ошибку, незаметную с первого взгляда.

Пример:«Дважды два пять»

Геометрические софизмы - это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, связанную с геометрическими фигурами и действиями над ними и задачи (оптических иллюзий) на перестановку фигур.

 .Пример: «Спичка длиннее, чем телеграфный столб, причем вдвое».

Основные ошибки, на которых строятся софизмы:

1. Деление на 0;
2. Неправильные выводы из равенства дробей;
3. Нарушения правил действия с именованными величинами;
4. Проведение преобразований над математическими объектами, не имеющими смысла;
5. Неравносильный переход от одного неравенства к другому;
6. Выводы и вычисления по неверно построенным чертежам.

    В ходе своей работы я познакомилась с очень увлекательной темой, о которой раньше только   слышала поверхностно, научилась решать некоторые софизмы, находить в них ошибки, изучила различные классификации математических софизмов, выступила с сообщением по данной теме перед своими одноклассниками с презентацией проекта, научилась сама составлять софизмы.  Результатом моей работы является выступление на школьной конференции «Защита проектов» и сборник задач «Математические софизмы», который я составила для учеников увлечённых математикой.

 

Оглавление

Введение …………………………………………………….. стр. 3

1.Теоретическая часть

1. 1. История софизмов …………………………………..стр. 4
   2. Что такое «софизм» …………………………………стр. 5
   3. Виды софизмов и их примеры……………………....стр. 6

2.Практическая часть

    2.1. Алгебраические софизмы ………………………….. стр. 9

    2.2. Арифметические софизмы ………………………….стр. 10

    2.3. Геометрические софизмы …………………………..стр. 11

3. Основные ошибки на которых строятся софизмы …….стр. 12

4. Вывод …………………………………………………….стр. 13

5. Заключение ……………………………………………….стр. 13

6. Литература ……………………………………………….стр. 14

7. Приложения………………………………………………стр. 15-22

 

 

                                         Введение

Чем больше учишься, тем больше знаешь.

Чем больше знаешь, тем больше забываешь.

Чем больше забываешь, тем меньше знаешь.

Чем меньше знаешь, тем меньше забываешь.

Но чем меньше забываешь, тем больше знаешь.

Так для чего учиться?

У нас в классе есть слабые ученики, которые до сих пор не знают таблицу умножения. И однажды учитель похвалил такого ученика, сказав, что он прав, что действительно, семью семь будет сорок семь, и доказала нам это. Вот так состоялось моё первое знакомство с софизмами. Меня заинтересовала эта тема, и я решила изучить тему софизмов, исследовать ошибки, на которых строятся математические софизмы, самой научиться составлять примеры софистических утверждений и их доказывать.

Тема «Софизмы» на сегодняшний день очень актуальна. «Софизмы» развивают логическое мышление, учат доказывать свою точку зрения. Детальный разбор софизмов помогает осознать ошибки, которые очень часто допускаются при выполнении различного рода заданий, осознанно усвоить математический материал. Это развивает наблюдательность, вдумчивость в изучаемый материал. Кроме всего вышесказанного разбор софизмов очень увлекателен.

Большинство софизмов известны очень давно, некоторые из них передаются устно из поколения в поколение. Я полагаю, что применение софизмов на уроках математики могли бы помочь вызвать интерес учащихся к предмету и разнообразить уроки.

Цель: Узнать, что такое математические софизмы.

Задачи проекта:           

1.     Познакомиться с понятием – софизм.

2.     Узнать виды математических софизмов.

3.     Рассмотреть примеры математических софизмов

4.     Понять где используются математические софизмы

5.     Научиться составлять свои математические софизмы,

6.     Создать сборник задач «Математические софизмы».

Проблема: мне хотелось бы узнать, смогу ли я путём некоторых рассуждений ввести окружающих в заблуждение, т.е. под силу ли мне самостоятельно составить математический софизм.

Гипотеза: софизм – это искусно замаскированные ошибки.

Предмет исследования: математические софизмы.

Методы исследования:

1. Нахождение и изучение материала

 2. Анализ полученной информации.

Значимость проекта: углубление знаний по математике и умений решать математические софизмы.

 

1. Теоретическая часть

1.1. История софизмов

Первые философы -  софисты жили в Древней Греции (V—IV вв. до нашей эры), но софизмы существовали задолго до их появления. Наиболее известные и интересные из софизмов были сформулированы в философских школах под влиянием Сократа. Однако принято считать, что термин «софизм» впервые ввел Аристотель, охарактеризовал софистику как мудрость мнимая, а не действительная.

Софисты – это мудрецы, которые учили граждан, приёмам ведения спора, красноречию. Задача «учителей мудрости» состояла в том, чтобы научить человека подтверждать или опровергать все, что угодно и выходить победителем из любой дискуссии: побеждает не тот, кто находится на стороне истины, а тот, кто лучше владеет приемами доказательства своей точки зрения. В своей работе они применяли различные логические, риторические и психологические приемы. Софисты утверждали, что все в мире субъективно и относительно.

1.2. Что такое «софизм»

Софизм (в переводе с греческого - мастерство, умение, хитрая выдумка, уловка, мудрость) — ложное умозаключение, которое при поверхностном рассмотрении кажется правильным. В обычном и распространенном понимании софизм — это умышленный обман, основанный на нарушении правил языка или логики.

В словарях и энциклопедиях я нашла определения софизма:

• «Большая советская энциклопедия»: софизм — логически порочное умозаключение, в котором ложные посылки выдаются за истинные или делается вывод с нарушением законов логики.
• «Толковый словарь русского языка», С. И. Ожегова: софизм — формально кажущееся правильным, но по существу ложное умозаключение, основанное на преднамеренно неправильном подборе исходных положений.
• «Толковый словарь», В. И. Даля: софизм — мудрствованье, ложный вывод, заключенье, сужденье, которому придан внешний вид истины. Софистическое рассуждение — ложное, ошибочное, под видом истинного.
• «Толковый словарь русского языка», Д. Н. Ушакова: софизм — формально правильное, но ложное по существу умозаключение, основанное на натяжке, на преднамеренно неправильном подборе исходных положений в цепи рассуждений.

На основании данных определений я сформулировала для себя определение софизма - это утверждение (умозаключение), выдаваемое за правильное, в котором допущена, умело замаскированная ошибка.

Обычно софизм обосновывает какую-нибудь заведомую нелепость. Например, софизм: «Рогатый».  «Что ты не терял, то имеешь; рога ты не терял, значит, у тебя рога».

И так софизмы — это логически неправильные рассуждения, которые используются с намерением ввести собеседника в заблуждение. Осмысление логических ошибок, которые содержались в софизмах Древней Греции, было важным моментом в развитии логики и культуры вообще, от решения общих проблем Вселенной (космоса, мироздания) к решению проблемам человеческой жизни, человеческих отношений.

Именно с софизмов началось осмысление и изучение доказательства и опровержения.

1.3. Виды софизмов и их примеры.

Существует два основных вида софизмов логические и математические.

В своей работе я рассматриваю только математические софизмы: геометрические, арифметические и алгебраические.

В математике очень много неожиданных и интересных софизмов, некоторые из них послужили толчком к новым открытиям. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях.

Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и алгебраических выражениях.

Пример1: “Неравные числа равны.”

Возьмем два неравных между собой произвольных числа а и b. Пусть их разность равна с, т. е. а-b = с. Умножив обе части этого равенства на а-b, получим (а-b)² = = c(a-b), a раскрыв скобки, придем к равенству a²-2ab + b² = = ca-cb, из которого следует равенство а²- аb - ас = аb -b² -bc. Вынося общий множитель а слева, и общий множитель b справа за скобки, получим а(а-b-с) = b(а-b-с). (1)

Разделив последнее равенство на (а-b-с), получаем, что а=b, другими словами, два неравных между собой произвольных числа а и b равны.

Разбор софизма: Здесь ошибка совершена при переходе от равенства (1) к равенству а = b. Действительно, согласно условию разность двух произвольных чисел а и b равна с, т. е. а-b = с, откуда а-b-с = 0. Можно записать равенство (1) в виде а-0=b-0. Переход от равенства (1) к равенству, а = b осуществляется путем деления обеих частей (1) на равное нулю число а-b-с = 0. Следовательно, здесь мы имеем деление нуля на нуль, которое не имеет смысла, поскольку равенство, а*0 = b*0 выполняется при любых а и b. Поэтому вывод, сделанный в софизме, что числа а и b равны, неверен.

Пример 2.«Любое число а равно меньшему числу b».

Рассмотрим  равенство: а=b+с. Умножу обе его части на а-b, получаю: a² - ab=ab+ac-b² -bc. Перенесу ас в левую часть: a² -ab-ac=ab-b² -bc. Вынесу общие множители в левой и правой части: a(a-b-c)=b(a-b-c). Разделив обе части равенства на a-b-с, получаю, что а=b, что и требовалось доказать.

Комментарий: делить обе части равенства на (a-b-c) нельзя, так как по определению a=b+c, следовательно (a-b-c)=0, а на ноль делить нельзя.

  Арифметические софизмы- это числовые выражения имеющие неточность или ошибку, незаметную с первого взгляда.

Пример 1. «Дважды два пять»

Рассмотрю равенство 4:4=5:5, вынесу в правой и левой части общий множитель за скобки, получаю: 4(1:1) = 5(1:1), так как множители 1:1 равны, то и 4=5, а 4=2*2, значит, 2*2=5.

В чём ошибка? Ошибка допущена при вынесении общего множителя.

Геометрические софизмы - это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.

Пример 1. «Спичка длиннее, чем телеграфный столб, причем вдвое».

Длину спички будет обозначать а, длину столба – б. Разность между этими величинами – c. получается, что b – a = c, b = a + c. Если данные выражения перемножить, получится следующее: b² – ab = ca + c². При этом из обеих частей выведенного равенства возможно вычесть составляющую bc. Получится следующее: b² – ab – bc = ca + c² – bc, или b (b – a – c) = - c (b – a – c). Откуда b = - c, но c = b – a, поэтому b = a – b, или a = 2b. То есть спичка и правда вдвое длиннее столба.

Комментарий: ошибка в данных вычислениях заключается в выражении (b – a – c), которое равно нулю.

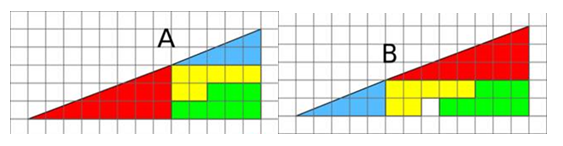
Пример 2.«Исчезновение клетки» (появление клетки) — известный класс задач (оптических иллюзий) на перестановку фигур.

Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при визуальном сохранении изначальных пропорций появляется дополнительная, не занятая ни одной частью, клетка.

 

Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади. Секрет в свойствах синего и красного треугольников. Это легко проверить если наложить верхнюю и нижнюю фигуры 13×5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. Визуально изгиба в гипотенузах практически незаметно. (Приложение 1)

Эту задачу изобрёл иллюзионист-любитель из Нью-Йорка Пол Карри в 1953. Однако принцип, заложенный в неё, был известен ещё в 1860-е году.

 

 

2. Практическая часть

Изучив данную тему, я решила сформулировать свои софизмы, доказать их и составить свой сборник задач «Математические софизмы».

2.1. Алгебраические софизмы

Пример 1 .«Семь равно пяти»

Рассмотрю равенство: 7 = 5+2. Умножу обе его части на 7-5, получаю:

49 – 35=35-25+14-10. Перенесу 14 в левую часть: 49-35-14=35-25-10. Вынесу общие множители в левой и правой части: 7(7-5-2)=5(7-5-2). Разделив обе части равенства на 7-5-2, получаю, что 7=5, что и требовалось доказать.

В чём ошибка? Пояснение:7-5-2=0, на 0 делить нельзя!

Пример 2. «Всякое положительное число является отрицательным»

Пусть k — положительное число. Очевидно, 3k-3 <3k (1). Возьму другое произвольное положительное число а и умножу обе части неравенства на (-а), получаю: – 3аk + 3а <–3аk. (2).  Вычитая из обеих частей этого неравенства величину (–3аk), получила неравенство 3а<0 , разделю обе части неравенства на 3, получаю а<0. Я доказала, что всякое положительное число является отрицательным

В чём ошибка? Пояснение: в софизме нарушено следующее правило: при умножении обеих частей неравенства на одно и то же отрицательное число знак неравенства меняется на противоположный.

Пример 3.«Уравнение 2х-6=0 не имеет корней»

Вынесу в левой части уравнения общий множитель, получаю 2(х-3) =0, разделим обе части уравнения на (х-3), получаем

2(х-3)/(х-3) =0/(х-3) и отсюда 2=0. Равенство не верное, уравнение решений не имеет.

В чем ошибка? При решении уравнения производим деление на х-3, а уравнение х-5=0 есть следствие уравнения 2х-6=0, а на ноль делить нельзя.

 

 

2.2. Арифметические софизмы

Пример 1.«Один сантиметр не равен десяти миллиметрам»

Возьму верное равенство:

1см = 10 мм.

Возведу его по частям в квадрат.

Получаю: 1см = 100 мм.

Известно, что если a=b, c=d, то ac=bd.

Применим это положение к равенствам   1см=10мм (1) и  10см=100мм(2)

Перемножая (1) и (2), получим   10 см=1000мм.

И, наконец, разделив последнее равенство на 10, получим  1 см=100 мм.

Таким образом, один сантиметр не равен десяти миллиметрам.

Где ошибка??

Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

Пример 2. «Семью семь сорок семь»

Рассмотрю равенство 49:49=47:47, вынесу в правой и левой части общий множитель за скобки, получаю: 49(1:1) = 47(1:1), так как множители 1:1 равны, то и 49=47, а 49=7*7, значит, 7*7=47.

В чём ошибка? Ошибка допущена при вынесении общего множителя.

Пример 3.  «Шесть равно десяти»

 Возьмем равенство 6+12-18=10+20-30.  Вынесем общие множители за скобку: 6(1+2-3) =10(1+2-3). Разделим на (1+2-3), отсюда 6=10.

Ошибка: 1+2-3=0, а на 0 делить нельзя.

Пример 4. «Семь умножить на четыре равно двадцать четыре».

Рассмотрим равенство 28-28=24-24. Вынесем за скобку общие множители: 28(1-1) =24(1-1). Разделим на (1-1), значит, 28 = 24, получаем 7*4=24. Ошибка: 1-1=0, а на 0 делить нельзя.

 

2.3. Геометрические софизмы

Пример 1. «Моя младшая сестра выше меня»(Приложение2)

Мой рост 175см, а рост моей младшей сестры 140см.

Рассмотрю два равенства:

175-140=35 и 175=35+140, перемножу их левые и правые части,получила:

175*175-140*175=35*35+35*140, вычту из обеих частей 175*35, получаю

175*175-140*175-175*35=35*35+35*140-175*35,

вынесу общие множители за скобки 

175(175-140-35)= -35(175-140-35) (1),

разделю обе части равенства на (175-140-35), получаю, что 175= -35, но35=175-140, значит 175=140-175, перенесу 175 из правой части в левую 175+175=140, 140- это рост сестры. Получила, что рост моей сестры равен 350 см. Она меня выше в два раза! Разве такое возможно?!

В чём ошибка? Ошибка в делении обеих частей равенства (1) на (175-140-35)=0.

Пример 2. «Загадочное появление» (Приложение 3)

Возьму квадрат разделю его на равные части шестью линиями. Разрежу квадрат по диагонали и сдвину обе части вдоль линии разреза. Замечаю, что появилась одна лишняя линия.

От куда она появилась?

Пояснение: если внимательно присмотреться или измерить длину новых линий, то увидим, что их длина короче предыдущих. Длина всех остатков и составляет появившуюся линию.

Пример 3. «Загадочное исчезновение» (Приложение 4)

Я взяла ромб, разделила его на равные части пятью линиями. Разрезала ромб по линии, соединяющей верхнюю точку первой линии, с нижней точкой последней линии и сдвинула обе части вдоль линии разреза. Вижу, что одна линия исчезла.

Куда исчезла пятая линия??

Пояснение: На первый взгляд не заметно, но если внимательно присмотреться или измерить длину новых линий, то увидим, что их длина длиннее предыдущих. Длина линии, которая исчезла, распределилась по оставшимся линиям.

Пример 4. «И овцы целы и волки сыты» (Приложение 5)

Когда я готовилась к данной работе и показала фокус своей семье с исчезновением клетки в прямоугольном треугольнике, мой дед Вова сказал мне, что знает фокус, только не с исчезновением, а с появление лишней клетки.

Он взял шоколадку и ножом разрезал её на четыре не равные части. Затем переставил их местами. Шоколадка осталась целой, а одна часть, самая маленькая, осталась лежать в сторонке. Он взял и съел её. Вот говорит:  «И овцы целы и волки сыты». Поэтому свой софизм я так и назвала «И овцы целы и волки сыты».

В чём ошибка? Положим рядом разрезанную шоколадку и неразрезанную.  Как видим, магии не произошло, разрезанная шоколадка стала меньше, её площадь уменьшилась ровно на площадь той части, которая осталась лишней. А визуально это не заметно.

Как завещал Ломоносов: «Если где-то убыло, значит, где-то прибыло. Ничего не исчезает в никуда и не появляется из ниоткуда» Закон сохранения вещества.

1. Основные ошибки, на которых строятся софизмы:

7. Деление на 0;
8. Неправильные выводы из равенства дробей;
9. Нарушения правил действия с именованными величинами;
10. Проведение преобразований над математическими объектами, не имеющими смысла;
11. Неравносильный переход от одного неравенства к другому;
12. Выводы и вычисления по неверно построенным чертежам.

2. Вывод

Изучив историю возникновения софизмов, рассмотрев ошибки, на которых строятся математические софизмы, проанализировав множество примеров, я пришла к выводу:

- математические софизмы учат нас внимательности;

- призывают нас учить теорию по математике, знать формулы и равносильные преобразования;

- верно выполнять чертежи при решении геометрических задач;

- развивают логическое мышление;

- помогают сознательному усвоению изучаемого материала;

- воспитывают вдумчивость, наблюдательность, критическое отношение к тому, что изучается.

Для меня исследовать софизмы оказалось очень интересным и увлекательным занятием.

Гипотеза, которую я ставила в начале работы: что софизм – это искусно замаскированные ошибки подтвердилась.

3. Заключение

    В ходе своей работы я познакомилась с очень увлекательной темой, о которой раньше только   слышала поверхностно, научилась решать некоторые софизмы, находить в них ошибки, изучила различные классификации математических софизмов, выступила с сообщением по данной теме перед своими одноклассниками с презентацией проекта, научилась сама составлять софизмы.  Результатом моей работы является выступление на школьной конференции «Защита проектов» (Приложение 6) и сборник задач «Математические софизмы», который я составила для учащихся увлечённых математикой (Приложение 7).

 

 

 

4. Литература:

1. https://znanio.ru
2. https://infourok.ru/
3. https://azbyka.ru
4. https://otvet.mail.ru
5. https://otherreferats.allbest.ru
6. https://ru.wikipedia.org/
7. http://pрtcloud.ru/
8. http://anadra.ru/sitemath/
9. https://ru.wikipedia.org/wiki

 

 

 

Полный текст статьи см. в приложении.

1. file0.docx.. 4,9 МБ
2. file1.pptx.. 4,4 МБ

Опубликовано: 19.12.2023