Математика через творчество: нестандартные задачи для младших школьников

Автор: Леончикова Светлана Андреевна

Организация: МБОУ СШ №71

Населенный пункт: город Воронеж

Математика — это не только сложные уравнения и формулы, но и мир, наполненный красотой, логикой и творчеством.

Современное образование все больше стремится объединить эти два аспекта, помогая младшим школьникам не только осваивать математические навыки, но и развивать креативное мышление.

Нестандартные задачи, основанные на творческом подходе, помогают детям видеть математику с разных сторон и применять её в повседневной жизни.

Способностью к творческому мышлению в какой-то мере обладает, наверное, каждый. Уже вначале жизни у человека проявляется настоятельная потребность самовыражения через творчество, человек учится мыслить творчески, хотя способность к такому мышлению не является необходимой для выживания. Творческое осмысление является одним из способов активного познания мира, и именно оно делает возможным прогресс, как отдельного индивида, так и человечество в целом. Тем не менее, не каждого человека мы можем назвать творческой личностью.

Творческая деятельность представляет высший уровень развития мышления человека, который обладает следующими способностями;

• получением результата, которого раньше никто не добивался;
• возможностью действовать различными путями, не зная, какой из них может привести к желаемому результату;
• априорной ( предварительной) неизвестностью способов, с помощью которых этот результат может быть достигнут;
• отсутствием достаточного опыта решения подобных задач;
• необходимостью действовать самостоятельно и без подсказки.

Множество примеров подлинно творческого мышления мы можем обнаружить у людей, занятых интеллектуальным трудом, причём это вовсе не обязательно должны быть чисто умственные, словесно логические. Творческой может быть и практическая деятельность, причём не только писателя, учёного, но и бизнесмена, рабочего, крестьянина, если они своим трудом создают нечто новое, уникальное, необычное.

Творчество – это, прежде всего умение, отказаться от стереотипов мышления, только в этом случае можно создать что-то новое. В этом отношении большие возможности имеются на уроках математики, в частности при решении нестандартных задач.

Нестандартная задача в отличие от традиционной не может быть непосредственно (в той форме, в которой она предъявлена) решена по какому-либо алгоритму. Такие задачи не сковывают ученика жёсткими рамками одного решения. Необходим поиск решения, что требует творческой работы мышления и способствующий его развитию. “Задача, которую вы решаете, может быть скромной, но если она бросает вызов вашей любознательности и заставляет вас быть изобретательными, то вы можете испытать ведущее к открытию напряжения ума и насладиться радостью победы”.

Решение нестандартных задач – процесс сложный. При решении таких задач дети встречают трудности. Это объясняется такими причинами: из-за неуверенности в своих возможностях и боязни их трудности, отсутствием необходимого для этого умения и навыков. Только при систематической работе можно достичь желаемого результата, поэтому обучением решению нестандартных задач занимаюсь с первого класса. Занятия проводятся в неделю один раз.

Обязательными при проведении занятий является соблюдение условий безоценочности, принятия, поддержки. Для реализации этих условий нужно восхищаться каждой идеей ребёнка, исключается всякая критика личности и деятельность детей, принимаются и выслушиваются все ответы, создаётся климат взаимного доверия. Использую принципы развивающего обучения: проблемность, диалогичность, индивидуализация.

Значение креативного подхода в обучении.

Креативные методы в обучении математики способствуют формированию у детей интереса к предмету. Когда учащиеся видят практическое применение математики в творческих заданиях, они становятся более мотивированными и активными в процессе обучения. Такие задачи развивают не только математические навыки, но и критическое мышление, способность к решению проблем и командную работу.

Занятия проводятся в форме игры, сказки, консультации, матбоя и др. Работают парами, в группах. Учащиеся читают задачу, обсуждают между собой, слушают мнения товарищей, спорят, отстаивают свои мнения, рассуждают, планируют работу. При такой форме работы все активно работают, все хотят выступать, объяснять свои решения.

Нестандартность задачи состоит не в её сложности, а в непривычности для учащихся. Такие задачи являются новыми, необычными для учащихся не вообще, а лишь в данных условиях. После решения большого количества нестандартных задач одного вида они теряют свою необычность для учащихся и превращаются в стандартные, у учащихся формируется алгоритм их решения, в некоторых случаях он доводится до автоматизма и выработки стереотипа в решении задач данного вида.

Нестандартные задачи представляют, как раз тот благодатный материал, при обучении которому у учащихся формируются творческие способности. Это умение является важнейшей стороной подготовки учащихся к дальнейшей практической и теоретической деятельности. Научить в школе решению всех задач, которые могут встретиться в жизни, невозможно: их количество практически необозримо.

Вот несколько примеров нестандартных задач, которые могут быть использованы на уроках математики:

 

1. Математическое творчество с рисованием

- Предложите детям нарисовать свою "математическую страну", где каждый элемент должен быть связан с математическими понятиями: например, дома в форме геометрических фигур, дороги, ведущие к числовым линиям, или деревья с листочками-уровнями (как в учебниках). Учащиеся могут представлять и обосновывать свои решения, демонстрируя понимание геометрии и чисел.

 

2. Числовые истории

- Попросите детей придумать и написать короткие рассказы, в которых главные герои — числовые символы. Например, «Приключения числа 7». Дети должны включить в историю математические операции и примеры, такие как прибавление, вычитание, умножение и деление. Это развивает согласованность мышления и позволяет визуализировать математические операции.

 

3. Игровые ситуации

- Создание игровых задач — это отличный способ привлечь внимание детей. Например, «Какой минимальный возраст для покупки 5 мороженых, если одно стоит 15 рублей, а у вас есть только 50 рублей?» Такие задачи побуждают детей к расчётам и оценке, а также развивают навыки финансовой грамотности.

 

4. Решение проблем через конструкцию

- Дайте учащимся задание построить конструкцию, используя предметы (блоки, палочки, пуговицы и т. д.) так, чтобы соблюдали определённые математические условия — например, тригонометрические отношения или свойства геометрических фигур. Затем они могут представить свои конструкции классу и объяснить, как они связаны с изучаемой темой.

 

1. 5.Решение задач с недостающими данными.

- “Мальчику купили игрушки: мишку и машину. Машина стоит 25 руб. Сколько стоят вместе?”.

Такие задания способствуют развитию у учащихся нешаблонного анализа.

 

1. 6.Нерешаемые задачи.

- Сначала дается задача. “У Кати было 5 кукол, у Светы- 1 кукла. Сколько кукол у девочек?”

А потом предъявляется нерешаемая задача: “У Кати было 5 кукол, у Светы 1 кукла. Сколько кукол у Веры?”

Развивается умение осуществлять анализ новой ситуации.

 

1. 7.Задания на определение закономерности.

“Вставь пропущенное число” 2 5 8 11?

Решение таких задач требует умения самостоятельно осуществлять анализ ситуации и формировать гипотезы преобразования данной ситуации.

 

1. 8.Задания для формирования умения проводить дедуктивные рассуждения: “Гитара – музыкальный инструмент. У Айсена дома музыкальный инструмент. Значит, у него дома гитара?”. Правильны ли рассуждения или нет. Если нет, то почему?

При решении подобных задач учащиеся должны проводить смекалку, догадаться, что задача вообще не решается или что в задаче есть лишние данные или данных не хватает. Проявлению сообразительности при выполнении подобных заданий способствует формированию такого качества, как гибкость мышления, которая играет важную роль в развитии творческого мышления.

С самого начала при решении нестандартных задач нужно приучить детей изображать отрезками любые объекты, о которых известно, делать таблицы, показать задачи инсценировкой.

 

1. 9.Моделирование ситуации с помощью чертежа, рисунка.

а) “Вася выше Коли и ниже, чем Сеня. Кто из мальчиков самый длинный?”

При анализе решения таких задач желательно сопроводить сюжет рисунком на доске и в тетрадях.

б) “Петя родился на 3 года раньше Вовы. Сейчас Пете 6 лет. Сколько лет Вове?” Для полной наглядности полезно написать первые 10 чисел и расположить буквы П и В рядом соответствующими числами.

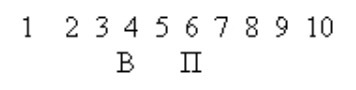
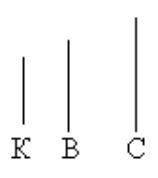
в) “5 мальчиков обменялись рукопожатием и подарили друг другу по одной своей фотографии. Сколько было рукопожатий? Сколько понадобилось фотографий?”

Такие задачи выясняются инсценировкой. Мальчики выходят к доске и пожмут друг другу руки, а ученики считают, сколько было рукопожатий. Потом обмениваются фотографиями. Ученики считают, сколько фотографий подарили.

г) “В клетке сидят цыплята и кролики. Всего у них 10 голов и 24 ноги. Сколько в клетке цыплят и сколько кроликов?”

Эта задача решается рисованием.

- Сколько всего было животных? Рисуйте отрезками без ног.

| | | | | | | | | |

- Прорисуйте по две ноги.

- Сколько ног все нарисовали? (20)

- Сколько осталось нарисовать? (4)

- Сколько кроликов? Сколько цыплят?

 

1. 10.«Математическое лото», например для закрепления состава числа, таблицы умножения или других тем.

- У каждого ученика есть карточка с ответами (например, числами 12, 15, 20 и т.д.). Учитель (или ведущий ученик) достаёт карточку с примером («3 х 4», «5 х 3», «10 + 10»). Учащиеся должны найти на своей карточке правильный ответ и закрыть его фишкой (крышкой от бутылки для воды). Выигрывает тот, кто первый закроет всю карточку.

 

1. 11.«Шпионские коды», например для развития логики и навыков порядкового счета.

- Учитель объявляет, что каждую букву алфавита можно зашифровать числом (А=1, Б=2 и т.д.). Затем дети получают закодированные послания, которые нужно расшифровать, например: «3, 1, 20, 1» (ОТВЕТ: КАТЯ). Можно усложнить, введя простые операции: «(5+1), (10-9), (2*4)» (ОТВЕТ: ЕЖИ).

 

1. 12. «Строим мост» (командная игра). Это решение задач в условиях ограниченных ресурсов.

Класс делится на команды. Каждая команда получает «стройматериалы» (например, 20 листов бумаги А4, 1 метр скотча, ножницы). Задача: построить мост между двумя столами, который выдержит вес учебника. Условие: мост должен быть не короче 50 см и не иметь других опор. Дети должны рассчитать прочность, длину, распределить материалы, что напрямую связано с геометрией и инженерным мышлением.

 

1. 13.«Магазин» для развития навыков сложения, вычитания и финансовой грамотности.

В классе организуется импровизированный «магазин». Товарам (игрушки, канцелярия) присваиваются ценники. Одни ученики становятся «покупателями» с определенным бюджетом (например, 100 условных рублей), другие — «продавцами». Задача покупателей — купить несколько товаров, не превысив бюджет, и правильно рассчитать сдачу. Задача продавцов — верно посчитать сумму покупки.

 

1. 14.«Живые графики». Это визуализация и понимание основ статистики и координатной плоскости.

- Учитель задаёт вопрос, на который можно ответить числом (например, «Сколько книг вы прочитали за лето?»). Дети выстраиваются в шеренгу в соответствии со своим ответом (например, те, кто прочитал 0 книг — слева, 1 книгу — рядом и т.д.). Получается «живая» столбчатая диаграмма. Затем можно обсудить, где «мода» (самый частый ответ), какое наименьшее и наибольшее значение.

 

1. 15. «Кулинарные математические тематики».

- Например, предложите детям составить рецепт печенья. Дайте им количество ингредиентов на 12 порций и попросите рассчитать, сколько ингредиентов понадобится на 6 или 24 порции. Это не только помогает в освоении пропорций, но и делает учебный процесс более практичным и вкусным.

Решая нестандартные задачи, дети сами приходят к выводу, что есть задачи, которые не решаются сразу одним действием, что надо анализировать, сравнивать, рассуждать.

 

Можно и дальше продолжать составлять оригинальный список. Главное надо понять, что решая нестандартные задачи, дети сами приходят к выводу, что есть задачи, которые не решаются сразу одним действием, что надо анализировать, сравнивать, рассуждать. Каждая нестандартная задача и каждая игра — это маленькая проблема, которая требует от учеников повышенной умственной активности, способствует развитию логико-математического и эвристического мышления.

 

Заключение

Каждая нестандартная задача – это маленькая проблема, которая:

- требует от учеников повышенной умственной активности и находчивости в поисках непроторенных путей решения;

- способствует развитию логико-математического продуктивного, эвристического мышления учащихся, активизации мыслительных операций, их самостоятельности, отточенности;

- вырабатывает ценные умственные качества: последовательность мысли, логичность, сообразительность, смекалку, то есть улучшает и повышает качество математической подготовки учащихся.

Нестандартные задачи и игровые методики — это мощный инструмент в руках учителя. Они позволяют сделать изучение математики увлекательным и креативным процессом. Важно, чтобы учителя не боялись экспериментировать и внедрять новые методики в свои занятия. Помните, что математика становится живой и интересной, когда она интегрируется с творчеством и игрой.

Одним из самых эффективных способов внедрения творческого подхода является игра. Игра создаёт естественную среду, в которой дети не боятся ошибаться, экспериментировать и находить неочевидные решения.

В то же самое время эти задачи не выходят за пределы программы начальных классов, а дают возможность учащимся активно работать на уроке.

 

 

Опубликовано: 14.11.2025