Урок по теме: «Координатная плоскость»
Автор: Лапчева Елена Дмитриевна
Организация: МБОУ СОШ №1
Населенный пункт: Владимирская область, г. Гороховец
Пояснительная записка.
Преподавание математики в 6 классе ведётся по учебнику С. М. Никольского. Урок по теме: «Декартова система координат на плоскости» является восьмым уроком в пятой главе «Обыкновенные и десятичные дроби». Основной метод, применяемый на уроке, - метод исследования, предполагающий построение обучения как творческого процесса открытия учениками нового знания. Урок построен на основе деятельностного подхода и технологии критического мышления. В ходе урока у учащихся формируются следующие умения: активная работа с текстами; работа с понятиями как особой формой знания; разработка алгоритмов действий, поиск способов решения поставленной проблемы и составления плана деятельности. Понятие координатной плоскости, кроме уроков математики, используется в других учебных предметах и в повседневной жизни. На данном уроке класс разбивается на 5 групп по 6 человек.
Сценарий урока по теме: «Декартова система координат на плоскости».
Тип урока: урок открытия нового знания.
Педагогическая технология: развитие критического мышления через чтение и письмо.
Формы организации обучения: групповая, коллективная, индивидуальная.
Цель: организация деятельности учащихся по открытию нового знания, создание условий для осмысления учебной информации по теме: «Декартова система координат на плоскости», развитие мыслительных навыков учащихся, необходимых не только в учебе, но и в дальнейшей жизни.
Учебные задачи, направленные на развитие учащихся:
- в личностном направлении:
- формирование уважительного отношения к другому человека, его мнению;
- формирование у учащихся готовности к самообразованию;
- формирование коммуникативной компетентности в общении со сверстниками.
- в метапредметном направлении:
- умение формулировать гипотезы и понимать необходимость их проверки;
- умение соотносить свои действия с планируемыми результатами;
- умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах и в окружающей жизни;
- умение находить в различных источниках информацию, необходимую для решения математических проблем и представлять её в понятной форме.
- в предметном направлении:
- овладение базовым понятийным аппаратом как важнейших математических моделей (координатная плоскость), позволяющих описывать и изучать реальные процессы и явления;
- умение работать с математическим текстом (анализировать и извлекать необходимую информацию), грамотно применять математическую символику и терминологию;
- развитие навыков построения координатной плоскости, точек на координатной плоскости; умение определять координаты точек.
Техническое обеспечение:
- компьютер для учителя;
- интерактивная доска;
- проектор;
- карточки с текстом. • Технологическая карта урока
|
№ |
Этап урока |
Деятельность учителя |
Деятельность ученика |
Формируемые УУД |
|
1. |
Этап самоопределение к деятельности |
Приветствует учащихся, мобилизует внимание детей.
|
Приветствуют учителя, организуют свое рабочее место, демонстрируют готовность к уроку. |
Личностные: самоопределение. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
|
2. |
Этап актуализации
|
Учитель предлагает рассмотреть следующие предметы: 1 группа: глобус 2 группа: шахматная доска 3 группа атлас с географическими картами, 4 группа: историческая карта 5 группа: билет в кинотеатр Задаёт вопрос: «Как вы думаете, какую профессию должен иметь человек, чтобы дать наиболее полную информацию об этих предметах?», «Какую информацию может получить человек данной профессии, исследуя данные предметы?». |
Каждая группа рассматривает свой предмет, формулирует ответ: учитель географии или истории, археолог, лётчик, моряк, учёный. |
Личностные: - формирование индивидуальных учебно-познавательных мотивов; - умение ясно понимать смысл поставленной задачи; - умение ясно, точно, грамотно излагать свои мысли в устной форме, выстраивать аргументацию. Метапредметные: - умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; - формирование умения принимать учебную задачу урока; - умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. Предметные: формулирование учащимися темы, цели урока и вопросов по теме. |
|
3. |
Этап проблематизации
|
Обращает внимание учащихся на объект, изображенный на интерактивной доске (Слайд 2) - прямоугольную систему координат с отмеченной точкой. Просит сравнить предметы, которые они исследовали с новым объектом. Обобщает ответы учащихся и сообщает, что математик сказал бы, что у всех этих предметов присутствует система координат, которая позволяет определить местоположение объекта. |
Выясняют, что заданная на данном предмете система координат позволяет определить местоположение города на карте или глобусе, фигуры на плоскости шахматной доски, человека в зрительном зале, точки на координатной плоскости. Выясняют, что координатная плоскость является математической моделью для всех рассмотренных предметов. |
|
|
4. |
Этап целеполагания |
Предлагает каждой группе сформулировать тему урока, вопросы по освоению темы. Организует беседу по выявлению темы урока. Показывает (Слайд 3), на котором записаны тема и вопросы, сформулированные учителем. Отмечает те вопросы, которые сформулировали учащиеся. Обращает внимание учащихся на те, вопросы, которые им не удалось сформулировать. Записывает на доске вопросы, которые дополнительно сформулировали учащиеся. |
Формулируют тему урока и вопросы по освоению данной темы. Тема: Декартова система координат на плоскости. Вопросы: 1. Что такое система координат? 2. Что такое координатная плоскость? 3. Как определить координаты точки на координатной плоскости? 4. Как отметить в координатной плоскости точку с заданными координатами? 5. Кто ввёл понятие координат на плоскости? |
|
|
5. |
Этап моделирования |
Предлагает описать рисунок, выделить важные математические объекты и постараться дать определения этим объектам (Слайд 2). Предлагает сформулировать гипотезу, как определить координаты точки на координатной плоскости, используя подсказки. Все гипотезы вывешиваются на доске. Предлагает выяснить, чья гипотеза оказалось верной и найти ответы на поставленные в начале урока вопросы. |
Высказывают свои предположения, дополняют друг друга, опираясь на собственный опыт, формулируют определения. Выясняют, что на рисунке изображены две взаимно перпендикулярные координатные прямые, которые пересекаются в точке О - начале отсчёта. На плоскости отмечена точка. Формулируют гипотезу определения координат точки на координатной плоскости: Для определения координат точки надо провести через нее две прямые, параллельные координатным осям. |
Личностные: - умение ясно понимать смысл поставленной задачи; - умение ясно, точно, грамотно излагать свои мысли в устной форме. Метапредметные: формирование умения принимать учебную задачу урока. Предметные: повторение темы «Координатная прямая», определение учебной задачи. |
|
6. |
Этап конструирования |
Организует работу учащихся с учебным текстом (Приложение 1). Индивидуальное задание: 1. Возьмите лист с текстом «Как и где можно встретить две координатные прямые» 2. Прочитайте внимательно текст. 3. Выделите в тексте математические понятия. Рядом с понятием, которое вы уже знали, поставьте знак «+», а с тем, которое узнали в процессе работы с текстом, знак «-». Заполните таблицу «Знаю, узнал» (Приложение 2). Групповое задание: Обсудите результат выполнения задания в группе. Исправьте, если это необходимо, свои таблицы. Учитель просит озвучить результат (Слайд 4). Коллективное задание: Сформулируйте определение «новых понятий». Если испытываете затруднения, найдите в тексте определения (Слайд 5), Индивидуальное задание: 1. Возьмите таблицу и текст так, чтобы цвета совпадали. 2. Используя текст, составьте алгоритм и запишите его в таблицу (Приложение 3): 1) построения координатной плоскости (желтый или белый лист) 2) построения точки по заданным координатам (красный, синий лист) 3) определения координат заданной точки (зелёный, белый лист) Групповое задание: Приём «ЗИГЗАГ»: Учитель просит учащихся собраться в другие группы, выполнявших задание на листе одного и того же цвета. Сравнить полученные алгоритмы. Исправить ошибки, если они имеются. Затем вернуться в группы и познакомить участников «старой» группы с результатами своей работы. |
Изучают текст учебника. Выделяют математические понятия, заполняют таблицу: «Знаю, узнал». Формулируют определения. Система координат – две взаимно перпендикулярные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них. Координатные оси – прямые, образующие систему координат. Ось ОХ – ось абсцисс, Ось OY - ось ординат. Координатная плоскость – плоскость, на которой выбрана система координат. Координаты точки на плоскости – это пара чисел, где на первом месте стоит абсцисса, а на втором – ордината точки. Составляют алгоритмы, заполняют таблицы:
Уточняют и исправляют составленные алгоритмы в «новых» группах. Знакомят учащихся «старой» группы с результатами своей работы.
|
Личностные: - формирование индивидуальных учебно - познавательных мотивов; - умение понимать смысл поставленной задачи; - умение ясно, точно, грамотно излагать свои мысли в устной и письменной форме; - умение грамотно аргументировать. Метапредметные: - формирование умения принимать учебную задачу; - умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять её в понятной форме; - понимать сущность алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Предметные: - развитие навыков построения точек на координатной плоскости; - умение определять координаты точек; - овладение базовым понятийным аппаратом как важнейших математических моделях; - умение работать с математическим текстом и применять математическую символику и терминологию. |
|
7. |
Этап презентации |
Предлагает учащимся представить результаты своей работы. Корректирует составленные учащимися алгоритмы. Возвращается к сформулированным в начале урока гипотезам. Выявляет, кто из учащихся правильно определил и записал координату точки в начале урока. |
Один из участников каждой группы зачитывает один из алгоритмов. Обсуждают варианты составленных алгоритмов. Исправляют ошибки. Вывешивают получившийся продукт (составленные алгоритмы) на доску. |
|
|
8. |
Первичное закрепление во внешней речи (обобщение затруднений во внешней речи). |
Организует усвоение учениками нового способа действий с проговариванием во внешней речи. Работа с учебником. Предлагает выполнить задание из учебника № 1062 и № 1063.
|
Выполняют задания в тетрадях и на доске (определяют координаты точек и отмечают точки по координатам), проговаривая ответы вслух.
|
Регулятивные: планирование, прогнозирование. Познавательные: построение логической цепочки рассуждений. Коммуникативные: уметь формулировать свое мнение и делать выводы. |
|
9. |
Подведение итогов. Рефлексия |
Подводит итоги урока. Отмечает, в какой мере достигнуты цели, выполнены задачи урока. Мы хорошо потрудились (Слайд 6-7). Спасибо за урок! |
По кругу высказываются одним предложением: -Я научился… -Мне было трудно… -Сегодня я узнал… -У меня получилось… -Теперь я могу… |
Коммуникативные: аргументация своего мнения Познавательные: контроль и оценка процессов результата деятельности. Регулятивные: адекватное понимание причин успеха и неуспеха. |
Приложение 1. Рассказ о том, как и где, используют две координатные прямые.
(Гельфман, Э. Г. Положительные и отрицательные числа в театре Буратино: учебное пособие по математике для 6-го класса / Э. Г. Гельфман. – Томск: Издательство Томского университета, 1993. – 320 с.)
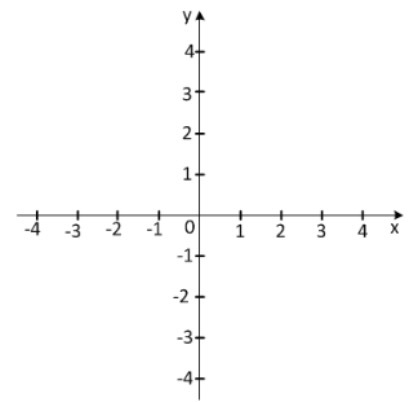
Знайка. Давайте-ка разберемся, как получен рисунок. Помоги мне, пожалуйста, Тюбик. Проведи на этом листе бумаге сначала одну прямую, а затем перпендикулярную к ней – другую. Получились две взаимно перпендикулярные прямые. Точку их пересечения обозначим буквой О. Выберем на каждой прямой положительное направление и одинаковые единичные отрезки.
Тюбик. Раньше мы работали с одной координатной прямой – с одной числовой (координатной) осью, а теперь у нас получилось две числовые координатные оси.
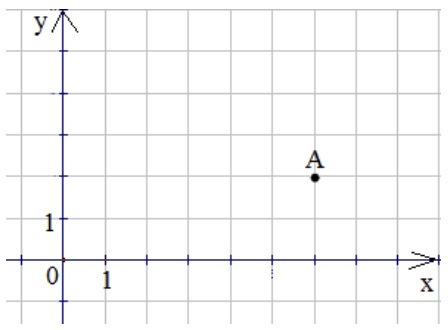
Знайка. Одну из них математики называют осью абсцисс, другую – ось ординат. Мы с тобой, Тюбик, построили прямоугольную систему координат. Плоскость, на которой задана такая система координат, называют координатной плоскостью. Ну-ка, Тюбик, выбери на координатной плоскости какую-нибудь точку.
Тюбик. Я выбрал точку А.
Знайка. Теперь, чтобы описать его местоположение, опусти из точки А перпендикуляры на каждую ось координат.
Тюбик. Провожу через точку А под прямым углом к осям две прямые.
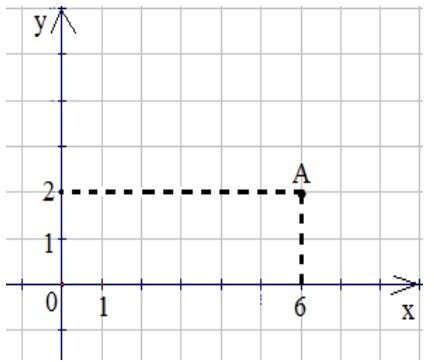
Знайка. На оси абсцисс основание перпендикуляра, соответствующую числу 6, а на оси ординат числу 2.
Число 6 называется абсциссой точки А, число 2 – ординатой точки А.
Тюбик. Ой, я догадался! Мою точку А можно описать двумя числами: 6 и 2!
Знайка. Верно! Абсцисса 6 и ордината 2 вместе называются координатами точки А и записываются так: А (6; 2)
При записи координат точки необходимо строго соблюдать следующий порядок: абсцисса всегда пишется на 1 месте, ордината – на втором. Координаты точки на плоскости – это пара чисел, в котором на первом месте стоит абсцисса, а на втором – ордината точки.
Тюбик. Понятно, это для того, чтобы не было путаницы. Ой, как интересно! Вот я нарисовал точки на координатной плоскости: Каждую из них я смогу описать с помощью двух чисел
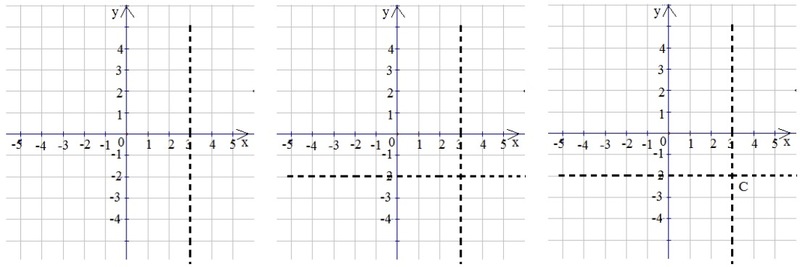
Знайка. И какую бы пару чисел я тебе не назвал, ты сможешь найти точку на плоскости, им соответствующую. Попробуй построить, например, точку С (3; -2)
Тюбик откладывает на оси абсцисс точку, соответствующую числу 3, на оси ординат – точку, соответствующую числу -2, проводит через эти точки перпендикуляры к осям, находит точку их пересечения и отмечает её буквой С.
Приложение 2. Таблицы «Знаю, узнал».
|
Знаю |
Узнал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 3. Бланки для алгоритмов.
|
|
Алгоритм построения координатной плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгоритм построения точки по заданным координатам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Алгоритм определения координат заданной точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 БЕСПЛАТНЫЕ семинары
БЕСПЛАТНЫЕ семинары





